(Foto: pixabay.com)
Pi ist gut, Tau ist besser
Die Kreiszahl Pi (π) kennt jeder, aber kennen Sie auch die mathematische Konstante Tau (τ)? Tau beschreibt das Verhältnis von Kreisumfang zum Kreisradius (τ = U/r). Oder einfacher ausgedrückt: Tau ist der Umfang des Einheitskreises (Radius = 1).
Von Markus Fleschutz · 📅 17. März 2019
Im Gegensatz zu Tau beschreibt Pi das Verhältnis von Umfang zum Durchmesser des Kreises (π = U/d). Problem dabei: Kreisformeln nutzen nie den Durchmesser, sondern immer den Radius. Dieser 'Geburtsfehler' führte dazu, dass in vielen Formeln "2π" vorkommt, was exakt Tau entspricht. Der genaue Wert von Tau lautet:
τ = 6.283185307179586476925286766559...
Mit Tau statt Pi lassen sich viele Formeln vereinfachen und der Einstieg in die Kreis-Geometrie fällt leichter. Hier ein paar Beispiele:
Kreisumfang
Die Berechnung des Kreisumfangs (U), also die Länge einer Kreislinie errechnet sich allein aus dem Kreisradius (r) wie folgt:
U = τ · r
Beispiel: ein Kreis mit 7 cm Radius hat einen Umfang von 43,9... cm.
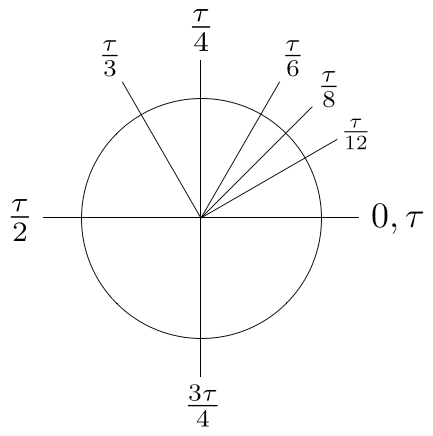
Mit Tau gelingt die Unterteilung des Kreisumfangs in Halbkreis, Viertelkreis, Achtelkreis, usw. völlig einfach und natürlich:
Kreisfläche
Die Berechnung der Kreisfläche (A) ergibt sich allein aus dem Kreisradius (r):
A = ½τ · r²
Beispiel: ein Kreis mit 7 cm Radius hat eine Fläche von 153,9... cm.
Kreissektor
Ein Kreissektor (auch Kreisausschnitt) ist in der Geometrie die Teilfläche einer Kreisfläche, die von einem Kreisbogen und zwei Kreisradien begrenzt wird. Ein Kreissektor wird durch Radius (r) und dem Winkel (α) bestimmt.
Bogenlänge: b = τ · r · (α / 360°)
Flächeninhalt: A = ½τ · r² · (α / 360°) oder A = (b · r) / 2
Umfang: U = 2·r + τ·r·(α / 360°)
Eigentlich ganz einfach: Nimm die Formel für Kreisumfang oder Kreisfläche und multipliziere sie mit dem Verhältnis des Winkels (α) zum Vollkreis (360°). Beim Umfang kommen natürlich noch die beiden Kreisradien hinzu.
Kreisring
Ein Kreisring wird gebildet aus zwei verschieden großen, konzentrischen (gleicher Mittelpunkt) Kreisen, wobei der kleinere vom größeren abgezogen wird. Ein Kreisring wird bestimmt durch Radius r1 (der größere) sowie Radius r2 (der kleinere).
Umfang: U = τ · (r1 + r2)
Flächeninhalt: A = ½τ · (r1² - r2²)
Volumen einer Kugel
Das Volumen (V) einer Kugel wird durch den Radius (r) wie folgt bestimmt:
V = ⅔τ · r³
Beispiel: eine Kugel mit 2 cm Radius hat ein Volumen von 33,5... cm³.
Oberfläche einer Kugel
Die Oberfläche (O) einer Kugel wird durch den Radius (r) wie folgt bestimmt:
O = 2τ · r²
Beispiel: eine Kugel mit 2 cm Radius hat ein Oberfläche von 50,3... cm².
Volumen eines Zylinders
Das Volumen (V) eines Zylinders wird aus Radius (r) und Höhe (h) bestimmt:
V = ½τ · r² · h
Beispiel: ein Zylinder mit 5 cm Radius und 10 cm Höhe hat ein Volumen von 785,4... cm³.
Oberfläche eines Zylinders
Die Oberfläche (O) eines Zylinders wird ebenfalls aus Radius (r) und Höhe (h) bestimmt:
O = τ · r² + τ · r · h
Beispiel: ein Zylinder mit 5 cm Radius und 8 cm Höhe hat eine Oberfläche von 408,4... cm².
Volumen eines Ellipsoid
Ein Ellipsoid ist die 3-dimensionale Entsprechung einer Ellipse. Das Volumen (V) eines Ellipsoid wird durch die Halbachsen (a), (b) und (c) bestimmt:
V = ⅔τ · a · b · c
Radiant
Der Radiant (Einheitenzeichen "rad") ist ein Winkelmaß, bei dem der Winkel durch die Länge des entsprechenden Kreisbogens im Einheitskreis angegeben wird. Wegen der Betrachtung des Kreisbogens zur Kennzeichnung des Winkels wird die Angabe „im Bogenmaß“ auch Bogenwinkel genannt.
Der Wertebereich beim Einheitskreis liegt zwischen 0 rad und τ rad (entspricht 360°, auch Vollwinkel oder Vollkreis genannt). In vielen Berechnungen der Physik und der Mathematik ist das Bogenmaß das zweckmäßigste Winkelmaß (beispielsweise bei der Winkelgeschwindigkeit sowie Sinus und Kosinus).
Hier die Umrechnung Radiant ↔ Grad beim Einheitskreis:
rad = deg · τ/360
deg = rad · 360/τ
Beispiel: ein Winkel von 90° entspricht 1,5707... rad beim Einheitskreis.
Summe aller Innenwinkel
In einem Viereck (egal ob Quadrat, Rechteck, Raute, Trapez oder Parallelogramm) beträgt die Summe aller Innenwinkel immer 360° oder τ rad:
α + β + γ + δ = 360°
In einem Dreieck (egal welche Form) beträgt die Summe aller Innenwinkel immer 180° oder ½τ rad:
α + β + γ = 180°
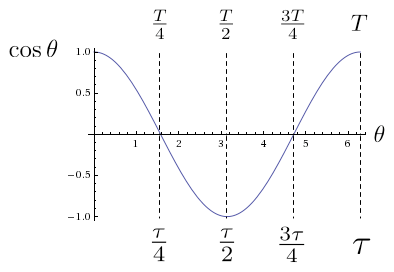
Sinus und Kosinus
Der Sinus eines Winkels (θ) ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus eines Winkels (θ) ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.
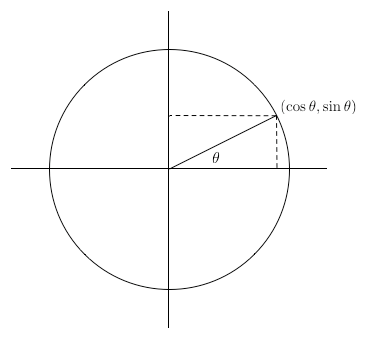
Mit der Hilfe von Tau lassen sich die Sinus- und Kosinus-Werte auch leichter verdeutlichen:
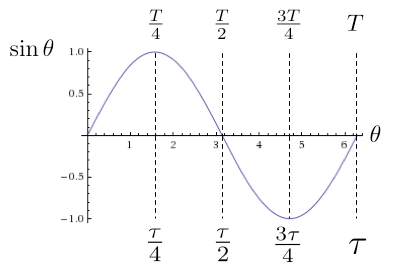
Winkelgeschwindigkeit
Die Winkelgeschwindigkeit ω→ wird durch einen Pseudovektor dargestellt, der die Richtung der Drehachse und die Schnelligkeit der Rotationsbewegung angibt. Die Richtung des Pseudovektors ist so orientiert, dass sie gemäß der Korkenzieherregel die Rotationsrichtung angibt. Der Betrag der Winkelgeschwindigkeit ω=|ω→| ist gleich der Ableitung des Rotationswinkels φ nach der Zeit t:
ω = dφ / dt
Bei konstanter Winkelgeschwindigkeit gilt daher:
ω = τ / T
denn in der Umlaufzeit T wird der Winkel τ durchlaufen.
Fazit
- Tau steht für den Vollkreis, Pi für den Halbkreis!
- Im Mathematik-Unterricht sollte Tau Vorrang vor Pi haben, da es leichter zu erlernen und logischer ist.
- Aus diesem Grund sollten auch alle mathematischen Hilfsmittel (Taschenrechner, Mathematik-Libraries, usw.) zusätzlich zu Pi auch Tau unterstützen.
- Bisherige mathematische Arbeiten müssen nicht auf Tau umgestellt werden. Durch das Ersetzen von 2π durch τ wird das Ergebnis weder besser noch schlechter.
- Auch bisherige Computerprogramme müssen nicht umgestellt werden: die Genauigkeit und Geschwindigkeit von 2π entspricht exakt τ.
- Und auch jene, die noch an Pi gewöhnt sind, müssen keine Umstellung befürchten. Sie verwenden einfach weiterhin wie gewohnt die Pi-Formeln.
Links
- 100.000 Nachkommastellen von Tau
- The Tau Manifesto (Englisch)
- The Pi Manifesto (Englisch)
- The Tau Day (Englisch)